"A mathematician is a person who can find analogies between theorems; a better mathematician is one who can see analogies between proofs; and the best mathematician can notice analogies between theories. One can imagine that the ultimate mathematician is one who can see analogies between analogies. "
------ Stefan Banach
Sometimes it is a good way to find analogies between algorithms in different fields. Here, I will talk about
Random Walk and
Markov Chain, especially their applications in three different fields: Search Engine, Image Retrieval and Visual Saliency.
1. Background Knowledge about Random Walk and Markov Chain
- Markov Chain: The random walk defined by a stochastic matrix;
- Chapman-Kolmogorov Equation: P(k)P(n-k) = P(n).
- Stochastic Matrix: a square matrix of non-negative entries, each of whose rows adds to 1;
- Probability Vector: a vector of non-negative entries that add to 1, and stochastic matrix is a square matrix with probability vectors for rows;
- Limiting Distribution: If p(n) = p(0)Pn converges to a limit vector p∞ as n → ∞, that vector is called the limiting distribution of the Markov chain;
- Stationary Distribution: A probability vector x is a stationary distribution (or equilibrium vector or steady state vector, or fixed point) for a Markov chain with transition matrix P if and only if p(n) = x ⇒ p(n+1) = x for any and all n. In words, once the distribution reaches a stationary distribution, it never changes.
- Transition Matrix: For a graph walk, the adjacency matrix of the graph tells which vertices you can move to.
We can represent the collection of all possible data sets as the vertices of a graph, with moves between data sets as edges. Choosing moves at random gives us a random walk on the graph.
Given a graph, what is the limiting distribution of the walk on that graph? How does the limiting distribution depend on the structure of the graph? If the limiting distribution is not uniform, is it possible to alter the graph walk to get a uniform distribution? How quickly does the walk reach its limiting distribution, and how does the convergence rate depend on the structure of the graph?
2. PageRank Algorithm in Search Engine
PageRank (PR) is a term that is used by Google. In simple terms, PageRank is how your site ranks with the Google search engine. So what is the basic algorithm and what does the algorithm mean to you? The algorithm:
PR(A) = (1 + d) + d (PR(T1)/C(T1) + … + PR(Tn)/C(Tn))
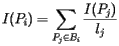
This may remind you of the chicken and the egg: to determine the importance of a page, we first need to know the importance of all the pages linking to it. However, we may recast the problem into one that is more mathematically familiar.
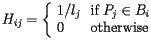
Notice that H has some special properties. First, its entries are all nonnegative. Also, the sum of the entries in a column is one unless the page corresponding to that column has no links. Matrices in which all the entries are nonnegative and the sum of the entries in every column is one are called stochastic; they will play an important role in our story.
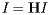
In other words, the vector I is an eigenvector of the matrix H with eigenvalue 1. We also call this a stationary vector of H.
Here's how the PageRank is determined. Suppose that page Pj has lj links. If one of those links is to page Pi, then Pj will pass on 1/lj of its importance to Pi. The importance ranking of Pi is then the sum of all the contributions made by pages linking to it. That is, if we denote the set of pages linking to Pi by Bi, then Let's first create a matrix, called the hyperlink matrix,
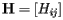
in which the entry in the ith row and jth column is We will also form a vector
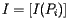
whose components are PageRanks--that is, the importance rankings--of all the pages. The condition above defining the PageRank may be expressed as A more detailed discussion about PageRank Algorithm can be found
here.
3. Graph Transduction in Image Retrieval
Given a set of objects X={x1, ..., xn} and a similarity functionsim: X×X→R+ that assigns a positive similarity value to each pair of objects. Assume that x1 is a query object (e.g., a query shape), {x2, ..., xn} is a set of known database objects(or a training set). Then by sorting the values sim(x1, xi) in decreasing order for i= 2, ..., n, we can obtain a ranking for database objects according to their similarity to the query. A critical issue is then to learn a faithful sim. A Schematic diagram is shown below.
Thus, the similarity of xi to the query x1, expressed as f(xi), is a weighted average over all other database objects, where the weights sum to one and are proportional to the similarity of the other database objects to xi:
f(xi) = P(i,1)f(x1)+P(i,2)f(x2)+ ... +P(i,n)f(xn)
Let w(i,j) = sim(xi, xj), for i,j = 1, ..., n, be a similarity matrix, then obtain a n×n probabilistic transition matrix P as a row-wise normalized matrix w. A new similarity measure s is computed based on P. Since s is defined as similarity of other elements to query x1, we denote f(xi) = s(x1, xi) for i = 1, ..., n. A key function is f and it satisfies We can see that those two formulations in PageRank and Graph Transduction are quite similar, because the mathematical foundations behind them are all Random Walk and Markov Chain. A more detailed discussion about Graph Transduction in Image Retrieval can be found
here.
4. Graph-based Visual Saliency
According to the analysis similar to PageRank Algorithm, we can calculate the stationary distribution of every nodes being visited when undergoing a random walk. If a cluster of nodes is different from its surroundings, then the probability of arriving at these nodes would be very small. Thus, this cluster of nodes is the visual saliency region. Results of Graph-based Visual Saliency is shown below:
Previous visual saliency research often utilize the contrast between center and surroundings both globally and locally. Edge cues are also introduced sometimes. However, this method treats every pixels (or superpixels, patches) as nodes in graph. The edges between nodes represent the similarity between two nodes. And the similarity measure could consist of color, texture and so on. Then an adjacent matrix can be obtained. A more detailed discussion about Graph-based Visual Saliency can be found
here.






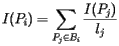
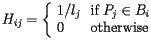
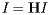
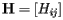 in which the entry in the ith row and jth column is We will also form a vector
in which the entry in the ith row and jth column is We will also form a vector 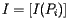 whose components are PageRanks--that is, the importance rankings--of all the pages. The condition above defining the PageRank may be expressed as A more detailed discussion about PageRank Algorithm can be found
whose components are PageRanks--that is, the importance rankings--of all the pages. The condition above defining the PageRank may be expressed as A more detailed discussion about PageRank Algorithm can be found 




